» » Rumus volume dan luas permukaan Bola

Rumus volume dan luas permukaan Bola

Postingan kemarin, saya membahas bagaimana rumus volume limas diperoleh. Sekarang saya akan membahas bagaimana rumus volume bola 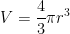{\displaystyle V=\frac{4}{3}\pi r^{3}}  diperoleh.
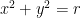
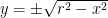
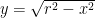
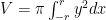
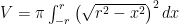
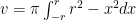
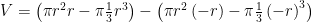
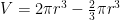
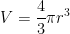
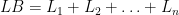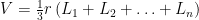
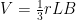
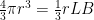
Diketahui  persamaan lingkaran dengan jari-jari r dengan titik pusat berada di titik asal pada kordinat kartesius adalah
x^2+y^2=r
solusi untuk 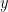y:
y=\pm\sqrt{r^{2}-x^{2}}
Sekarang perhatikan setengah lingkaran bagian atas
y=\sqrt{r^{2}-x^{2}}
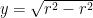fungsi y=\sqrt{r^{2}-r^{2}} kontinyu pada interval \left[-r,r\right]. Jika setengah lingkaran tersebut diputar, kita akan mendapatkan bola. Gunakan metode cakram untuk memperoleh volumenya.
V=\pi\int_{-r}^{r}y^{2}dx
V=\pi\int_{-r}^{r}\left(\sqrt{r^{2}-x^{2}}\right)^{2}dx
v=\pi\int_{-r}^{r}r^{2}-x^{2}dx
V=\pi r^{2}x-\pi\frac{1}{3}x^{3}|_{x=-r}^{x=r}
V=\left(\pi r^{2}r-\pi\frac{1}{3}r^{3}\right)-\left(\pi r^{2}\left(-r\right)-\pi\frac{1}{3}\left(-r\right)^{3}\right)
V=2\pi r^{3}-\frac{2}{3}\pi r^{3}
{\displaystyle V=\frac{4}{3}\pi r^{3}}
Viola, kita mendapatkan rumus volume bola.
Selanjutnya kita akan membahas rumus luas permukaan Bola 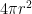4\pi r^{2}
Darimana rumus luas permukaan bola diperoleh?
Bayangkan sebua bola dengan jari-jari r tersusun dari potongan-potongan berbentuk limas sebanyak n→∞. Semua limas mempunyai tinggi r dan mempunyai titik puncak di titik pusat bola perhatikan gambar dibawah
Jadi permukaan bola tersusun dari alas-alas limas. Misalkan luas permukaan alas limas dari yang pertama sampai ke-n adalah L_{1},L_{2}\ldots,L_{n} maka luas permukaan bola adalah penjumlahan semua luas alas limas.
LB=L_{1}+L_{2}+\ldots+L_{n}.
Karena bola tersusun dari potongan-potongan limas maka volume bola adalah hasil penjumlahan semua volume limas.
V=\frac{1}{3}rL_{1}+\frac{1}{3}rL_{2}+\ldots+\frac{1}{3}rL_{n}
V=\frac{1}{3}r\left(L_{1}+L_{2}+\ldots+L_{n}\right)
V=\frac{1}{3}rLB
Telah kita bahas diatas bahwa volume bola adalah 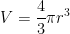{\displaystyle V=\frac{4}{3}\pi r^{3}}
\frac{4}{3}\pi r^{3}=\frac{1}{3}rLB
4\pi r^{2}=LB
Viola kita mendapatkan rumus permukaan bola 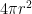4\pi r^{2}.
Share on Facebook
Share on Twitter
Share on Google+
Share on LinkedIn
close
==[ Klik disini 1X ] [ Close ]==